October 10, 2022

图神经网络学习

图神经网络从入门到入土

啊啊啊啊啊啊啊啊啊啊啊看不懂看不懂看不懂看不懂看不懂
不你可以看懂你可以看懂你可以看懂你可以看懂你可以看懂

一些概念

又要开始递归学习了……………………

卷积

如何通俗易懂地解释卷积？这篇文章讲的很清楚。

卷积的物理意义大概可以理解为：系统某一时刻的输出是由多个输入共同作用（叠加）的结果。
对图而言，用到的都是离散卷积。而离散卷积简单来讲本质上就是一种加权求和。

二维离散卷积的定义：

不同的图像处理函数（矩阵g）决定了输出图像（g与原始图像卷积之后的图像）是变得模糊还是锐利。
实际计算时会计算采用g翻转（上下左右翻转后）的矩阵与原图像的内积（对应点相乘相加）。

以前学信号的时候觉得这定义好抽象，根本不能理解，现在看了别人的解释感觉确实每一个公式都有它的来源……

神经网络

神经网络时由具有适应性的简单单元组成的广泛并进行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

M-P神经元模型

神经元接收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权链接进行传递，神经元接受到的总输入值将与神经元的阈值进行比较，然后通过激活函数（亦称响应函数）处理以产生神经元的输出。

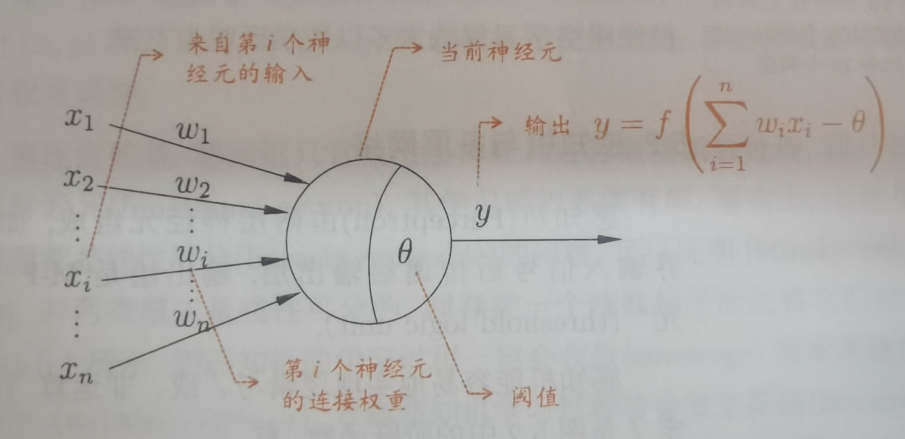
理想中的激活函数是阶跃函数，它将输入映射为0或1。但是由于阶跃函数不连续、不光滑，因此常用的激活函数是Sigmoid函数。

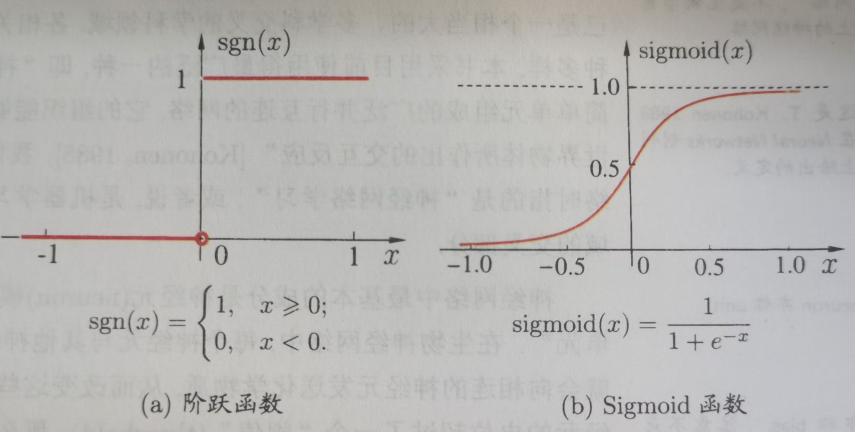
把许多个这样的神经元按一定的层次结构连接起来，就得到了神经网络。

事实上，我们只需要知道，神经网络是一个包含了许多参数的数学模型，这个模型是若干函数，例如相互（嵌套）带入而得。

CNN(Convolutional Neural Network 卷积神经网络)

对于卷积公式
在图像分析中，是 原始像素点(source pixel) ，是作用点，所有作用点合起来称为 卷积核(Convolution kernel) ，二者的卷积结果称为 目标像素(destination pixel) 。

CNN的核心在于它的kernel，kernel是一个个小窗口，在图片上平移，通过卷积的方式来提取特征。这里的关键在于图片结构上的平移不变性：一个小窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此CNN可以实现参数共享。

CNN中的卷积本质上就是利用一个共享参数的过滤器（kernel），通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取，加权系数就是卷积核的权重系数。

那么卷积核的系数如何确定的呢？是随机化初值，然后根据误差函数通过反向传播梯度下降进行迭代优化。这是一个关键点，卷积核的参数通过优化求出才能实现特征提取的作用，GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。

Graph embedding（图嵌入）

图分析任务

节点分类
基于其他标记的节点和网络拓扑来确定节点的标签(也称为顶点)。
链接预测
预测缺失链路或未来可能出现的链路的任务。
聚类
发现相似节点的子集，并将它们分组在一起。
可视化
有助于深入了解网络结构。

说明

真实的图（网络）往往是高维、难以处理的，为了将高维的图放到低维中去研究，图嵌入算法应运而生。
简而言之，图嵌入算法是为了降低高维图的维度，即降维技术。
首先根据实际问题构造一个D维空间中的图，然后将图的节点嵌入到d（d<<D）维向量空间中。嵌入的思想是在向量空间中保持连接的节点彼此靠近。

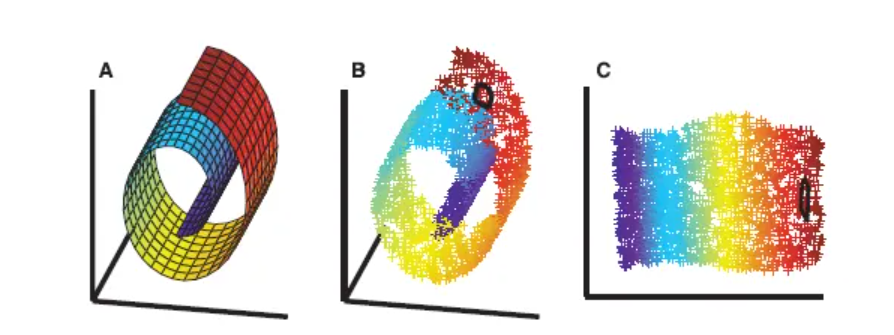
图嵌入的挑战

属性选择
节点的“良好”向量表示应保留图的结构和单个节点之间的连接。第一个挑战是选择嵌入应该保留的图形属性。考虑到图中所定义的距离度量和属性过多，这种选择可能很困难，性能可能取决于实际的应用场景。
可扩展性
大多数真实网络都很大，包含大量节点和边。嵌入方法应具有可扩展性，能够处理大型图。定义一个可扩展的模型具有挑战性，尤其是当该模型旨在保持网络的全局属性时。
嵌入的维数
实际嵌入时很难找到表示的最佳维数。例如，较高的维数可能会提高重建精度，但具有较高的时间和空间复杂性。较低的维度虽然时间、空间复杂度低，但无疑会损失很多图中原有的信息。

一些线代定义

度矩阵(degree matrix)

度矩阵是对角阵，对角上的元素为各个顶点的度。

邻接矩阵(adjacent matrix)

邻接矩阵表示顶点间关系。
行数和列数对应坐标写入两个节点的权重。
，其中是度矩阵，是邻接矩阵。

特征矩阵

给定，称多项式矩阵
为A的特征矩阵

其中是的特征值：
若存在和非零维向量，使得，则称为的特征值，向量称为的对应于特征值的特征向量。

拉普拉斯矩阵

(度矩阵邻接矩阵)

归一化

使得预处理的数据被限定在一定的范围内，从而消除奇异样本数据导致的不良影响。

何时使用？

对输出结果范围有要求
数据较为稳定，不存在极端的最大最小值
数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响。

几个学习概念

主动学习（active learning）
通过机器学习的方法获取到那些比较“难”分类的样本数据，让人工再次确认和审核，然后将人工标注得到的数据再次使用有监督学习模型或者半监督学习模型进行训练，逐步提升模型的效果，将人工经验融入机器学习的模型中。
监督学习（supervised learning ）
用一部分已知分类、有标记的样本来训练机器后，让它用学到的特征，对没有还分类、无标记的样本进行分类、贴标签。
半监督学习（semi-supervised learning）
有两个样本集，一个有标记，一个没有标记。综合利用有标记的样本和没有标记的样本，来生成合适的分类函数。
无监督学习（unsupervised learning ）
把相似度高的东西放在一起，对于新来的样本，计算相似度后，按照相似程度进行归类。
归纳学习（inductive learning）
训练集与测试集互斥
直推学习（transductive learning）
测试集（不带标签）包含在训练集中。有新样本时，需要重新计算。对于图而言，就是有新节点加入时，需要整张图重新计算。

理解：用一堆数据来训练模型，全部不给标签，让模型自己分类，这是无监督学习；给一部分标签，这是半监督学习；标签全给了，这是监督学习。当有一些新的数据需要得到它们的标签的时候，我得把这些新的数据并入原来的数据，整个重新训练模型，这是直推学习；可以根据原来的模型来预测这些数据的标签时，这是归纳学习。

换言之，监督不监督关注的是训练数据有没有标签，直推和归纳关注的是出现新数据时是需要并入旧数据重新训练模型还是根据原来的模型来预测这些数据的标签

为什么直推学习是半监督学习：原来的数据（一部分有标签或者全都有标签），新数据没有标签，新数据并入原来的数据后，一定会造成所有数据变成一部分有标签而一部分没有标签，这就是半监督学习。

那如果原来的数据全没有标签？为什么不能是无监督学习？

纯半监督学习：对于新数据不再重新训练模型，而是直接预测。（这是属于归纳学习吧

经过学长提醒才关注这几个概念并且搞清楚的呜呜呜呜呜

GCN(Graph Convolutional Network 图卷积网络)

来源

为什么要研究GCN？因为CNN无法处理拓扑图，只能处理图像那样规整的矩阵，无法卷积一个拓扑图。而我们又希望在拓扑图上有效地提取空间特征来进行机器学习，就需要研究GCN。

提取拓扑图的空间特征，在vertex domain(spatial domain)（空间维度）和spectral domain（图谱维度）实现目标是两种主流的方式，而后者就是GCN的理论基础。

Spatial domain

提取拓扑图上的空间特征，那么就把每个顶点相邻的neighbors找出来。

这种方法的主要缺点：

每个顶点提取出来的neighbors不同，计算处理必须针对每个顶点
提取特征的效果可能没有卷积好

Spectral domain

这是借助图谱的理论来实现拓扑图上的卷积操作。图谱维度将问题转换为频域分析，不再需要node-wise的处理。

简单理解

0x00 定义

大多数图神经网络模型都有一个共同的通用架构，这些模型称为GCN。

对于这些模型，目标是学习一个图（）上的信号/特征函数，这个图有以下输入：

每个节点有一个特征值，生成一个特征矩阵（一个维的矩阵），其中是节点个数，是输入的特征数。
一个描述各个节点关系（图的结构）的矩阵，通常是邻接矩阵

生成一个输出（一个特征矩阵，其中是每个节点的输出特征值）。

每个神经网络层都可以写成非线性函数
其中，是层数。具体模型的不同仅取决于如何选择。

0x01 举个例子

考虑下面这个简单的逐层传播规则形式：

是第层神经网络层的系数矩阵，是一个非线性激活函数（如）。虽然这个模型很简单，但它已经很强大。

当然，这个模型有几个局限性：

只使用的话，由于的对角线上都是0，所以在和特征矩阵相乘的时候，只会计算一个node的所有邻居的特征的加权和，该node自己的特征却被忽略了。因此，我们可以做一个小小的改动，给加上一个单位矩阵，这样就让对角线元素变成1了。
是没有经过归一化的矩阵，这样与特征矩阵相乘会改变特征原本的分布，产生一些不可预测的问题，比如邻居节点多的节点倾向于有更大的影响力。所以我们对做一个标准化处理。首先让的每一行加起来为1，我们可以乘以一个的逆，就是度矩阵。我们可以进一步把D的拆开与相乘，得到一个对称且归一化的矩阵

基于上述改进，我们得到了最终的层特征传播公式：

其中，是单位矩阵，是的对角节点度矩阵。
相当于给层的所有节点的embedding做了一次线性变换。
左乘以邻接矩阵表示对每个节点来说，该节点的特征表示为邻居节点特征相加之后的结果。

点形式：，即聚合邻居节点的特征然后做一个线性变换。

0x10 空手道俱乐部的embedding

这里的embedding我暂且理解为空间特征（不知道对不对，没找到解释这是什么意思）

图和视频在GRAPH CONVOLUTIONAL NETWORKS，我就不抄过来了（doge

采用一个随机的系数矩阵，甚至在训练权重之前我们只需要插入图形的邻接矩阵，然后让（即单位矩阵，因为我们没有任何节点特征），以这些作为模型输入。~~后面看原文吧，怎么翻都感觉很奇怪啊啊啊~~ The 3-layer GCN now performs three propagation steps during the forward pass and effectively convolves the 3rd-order neighborhood（3阶邻域） of every node (all nodes up to 3 “hops”（跃点） away). Remarkably, the model produces an embedding of these nodes that closely resembles the community-structure of the graph (see Figure below). Remember that we have initialized the weights completely at random and have not yet performed any training updates (so far)!

GCN为什么这么强？
我们可以通过将GCN模型解释为一个在图上的广义可微的Weisfeiler-Lehman算法来阐明这一点。

对于所有节点：

得到的邻居节点的特征值
更新节点特征，理想情况下，是一个injective hash function（简而言之，此哈希不能找到碰撞）

重复上述步骤次或直到收敛。

在实践中，Weisfeiler-Lehman算法为大多数图形分配了一组独特的特征。这意味着每个节点都分配有一个特征，该特征唯一地描述了它在图形中的角色。例外情况是高度规则的图形，如网格，链等。对于大多数不规则图，此特征分配可以用作图同构的检查（即两个图是否相同，直到节点的排列）。

回到我们的图卷积逐层传播规则（为向量形式）：

是节点的邻居节点的索引，是边的归一化常量，它源于我们在GCN模型中使用的对称归一化邻接矩阵。我们现在看到，这个传播规则可以被解释为可微分和参数化的（因为是原始Weisfeiler-Lehman算法中使用的哈希函数的变体）。如果我们现在选择一个适当的非线性并初始化随机权重矩阵，使其正交，则这个规则会在实践中变得更稳定（也要归功于）。

0x11 半监督学习

由于模型中的所有内容都是可微分和参数化的，因此我们可以添加一些标签，训练模型并观察嵌入如何反应。
我们只需要为每个类标记一个节点，并开始训练几次迭代。（看原文视频）

缺陷

GCN需要将整个图放到内存，比较耗内存，不能处理大图。
在训练时需要知道整个图的结构信息（包括待预测的节点）

GraphSAGE

来源

GCN输入了整个图，训练节点收集邻居节点信息的时候，用到了测试和验证集的样本，我们把这个称为Transductive learning。
然而，我们所处理的大多数的机器学习问题都是Inductive learning，因为我们刻意的将样本集分为训练/验证/测试，并且训练的时候只用训练样本。这样对图来说有个好处，可以处理图中新来的节点，可以利用已知节点的信息为未知节点生成embedding，GraphSAGE就是这么干的。

总的来说，GraphSAGE用于归纳节点的embedding，它利用节点特征来学习泛化到未知节点的embedding函数。当然，GraphSAGE也可以用于没有节点特征的图，只利用图的结构特征（如节点度数）。
GraphSAGE的关键思想在于如何从节点的本地邻域（如邻居节点的度数或文本属性）聚合特征信息。

简单理解

GraphSAGE是一个Inductive Learning框架，具体实现中，训练时它仅仅保留训练样本到训练样本的边，然后包含Sample和Aggregate两大步骤

Sample
对邻居的个数进行采样
Aggregate
拿到邻居节点的embedding之后如何汇聚这些embedding以更新自己的embedding信息

下图展示了GraphSAGE学习的一个过程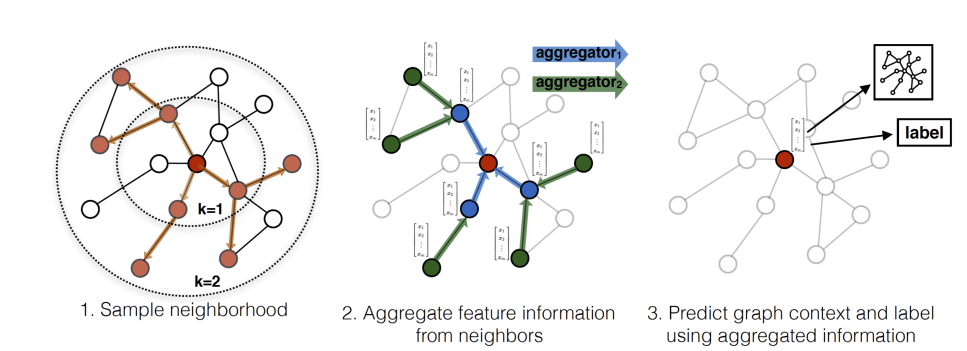

对邻居采样
采样后的邻居embedding传到节点上来，并使用一个聚合函数聚合这些邻居信息以更新节点的embedding
根据更新后的embedding预测节点的标签

下图详细说明了一个训练好的GrpahSAGE是如何给一个新的节点生成embedding的（即一个前向传播的过程），如下算法图：

首先，(line1)算法首先初始化输入的图中所有节点的特征向量，(line3)对于每个节点，拿到它采样后的邻居节点后，(line4)利用聚合函数聚合邻居节点的信息，(line5)并结合自身embedding通过一个非线性变换更新自身的embedding表示。

注意到算法里面的，它是指聚合器的数量，也是指权重矩阵的数量，还是网络的层数，这是因为每一层网络中聚合器和权重矩阵是共享的。网络的层数可以理解为需要最大访问的邻居的跳数(hops)。

给定一组输入节点，首先对所需的邻域进行向前采样（直到深度K），然后运行内部循环（line3），而不是迭代所有节点。

GraphSAGE Sample

采用定长抽样的方法。
具体来说，定义需要的邻居个数，然后采用有放回的重采样/负采样方法达到。保证每个节点（采样后的）邻居个数一致，这样是为了把多个节点以及它们的邻居拼接成Tensor送到GPU中进行批训练。

聚合器

图的邻居节点是没有自然顺序的，因此，聚合函数必须对一组无序的向量进行操作。
理想情况下，聚合函数是对称的（即输入的排列不变），同时仍可训练并保持高表示能力。
对称性可以确保我们的神经网络模型可以被训练并应用于任意排序的邻居节点特征集。

Mean Aggregator

和GCN做法基本一致

LSTM Aggregator

Applies LSTM to a random permutation of neighbors.
本质上是不对称的。

Pooling Aggregator

原则上，任何对称向量函数（如逐元素均值）都可以用来代替最大算子。开发测试中发现最大和平均没有显著差异。

总结

优点

利用采样机制，解决了GCN必须要知道全部图的信息问题，克服了GCN训练时内存和显存的限制。即使对于未知的新节点，也能得到其表示
聚合器和权重矩阵的参数对于所有的节点是共享的
模型的参数的数量与图的节点个数无关，这使得GraphSAGE能够处理更大的图
既能处理有监督任务也能处理无监督任务

缺点

没有考虑到不同邻居节点的重要性不同
聚合计算的时候邻居节点的重要性和当前节点也是不同的

GAT

来源

为了解决GNN聚合邻居节点的时候没有考虑到不同的邻居节点重要性不同的问题，GAT借鉴了Transformer的idea，引入masked self-attention机制，在计算图中的每个节点的表示的时候，会根据邻居节点特征的不同来为其分配不同的权值。

简单理解

对于输入的图，一个graph attention layer如图所示

Input features:
Importance of to :

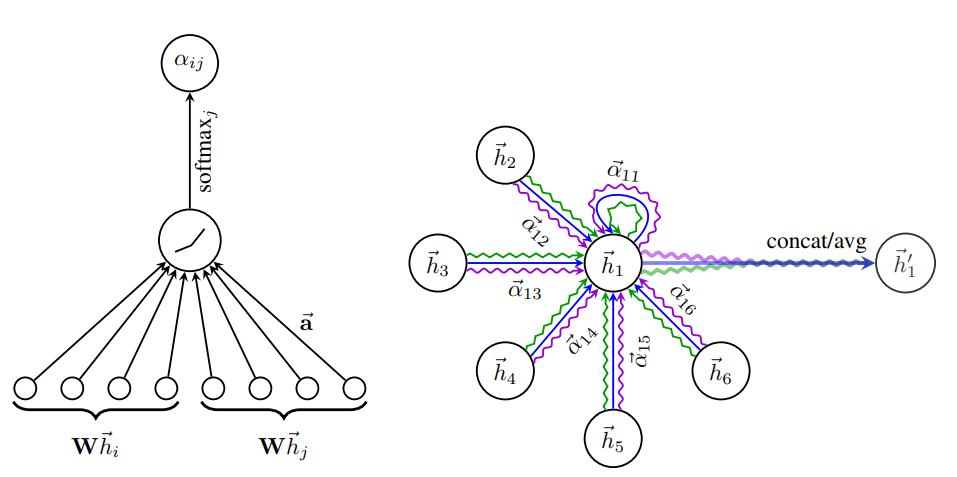
其中采用了单层的前馈神经网络实现，计算过程如下（注意权重矩阵对于所有的节点是共享的）：

计算完attention之后，就可以得到某个节点聚合其邻居节点信息的新的表示，计算过程如下：

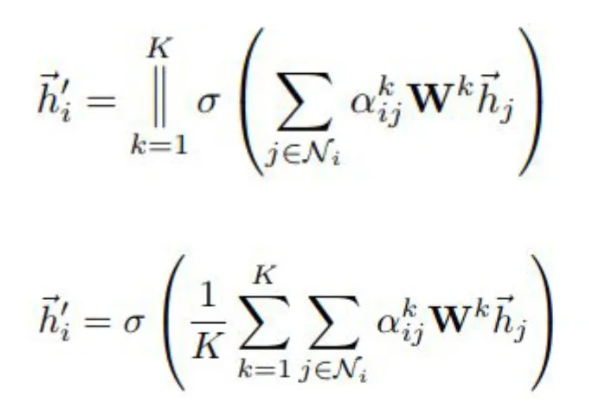
为了提高模型的拟合能力，还引入了multi-attention机制，即同时使用多个计算self-attention，然后将计算的结果合并（连接或者求和）：

此外，由于GAT结构的特性，GAT无需使用预先构建好的图，因此GAT既适用于Transductive Learning，又适用于Inductive Learning。

优点

训练GCN无需了解整个图结构，只需知道每个节点的邻居节点即可
计算速度快，可以在不同的节点上进行并行计算
既可以用于Transductive Learning，又可以用于Inductive Learning，可以对未见过的图结构进行处理

参考链接：
https://zhuanlan.zhihu.com/p/30994790
http://tkipf.github.io/graph-convolutional-networks/
https://blog.csdn.net/qq\_42189083/article/details/103407753
https://zhuanlan.zhihu.com/p/136521625
https://zhuanlan.zhihu.com/p/62629465
《机器学习》，周志华
https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf
https://zhuanlan.zhihu.com/p/136521625
https://arxiv.org/pdf/1710.10903.pdf
https://github.com/thunlp/GNNPapers/blob/master/README.md

关于本文

本文作者云之君, 许可由 CC BY-NC 4.0.