March 27, 2022

密码学习

~~公式渲染有点寄。。。。。总之是一堆问题。。。等有闲心了再整………………~~
二编：公式渲染搞好了，但是不知道为什么不渲染表格边框……吐血了

记录一些可能会用到的密码。

古典密码

仿射密码

加密函数：，其中

X表示明文按照某种编码得到的数字
a和m互质
m是编码系统中字母的数目

加密

解密函数：
其中是a对m的乘法逆元，即gmpy2.invert(a,m)
注意在括号外，不同于加密函数

解密

Playfair

加密方法如下：
1.选取一串英文字母，除去重复出现的字母，将剩下的字母逐个逐个加入 5 × 5 的矩阵内，剩下的空间由未加入的英文字母依 a-z 的顺序加入。注意，将 q 去除，或将 i 和 j 视作同一字。
2.将要加密的明文分成两个一组。若组内的字母相同，将 X（或 Q）加到该组的第一个字母后，重新分组。若剩下一个字，也加入 X 。
3.在每组中，找出两个字母在矩阵中的地方。
4.若两个字母不同行也不同列，在矩阵中找出另外两个字母（第一个字母对应行优先），使这四个字母成为一个长方形的四个角。

若两个字母同行，取这两个字母右方的字母（若字母在最右方则取最左方的字母）。
若两个字母同列，取这两个字母下方的字母（若字母在最下方则取最上方的字母）。
新找到的两个字母就是原本的两个字母加密的结果。

Polybius/棋盘密码

常用码表：

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I/J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

使用5个字符作为密文，每一个明文字母加密得到两个字符。所以其特征是密文只有5个字符，且加密后的密文长度是明文的2倍。

维吉尼亚密码

破译维吉尼亚密码的关键在于它的密钥是循环重复的。 关于密钥长度，可以使用卡西斯基实验和弗里德曼实验来取。

曲路密码

事先约定密钥（行列数以及曲路路径）。按照规定行列填入明文，按照曲路路径顺序写出密文。

列位移加密

将明文填入表（约定行列数），按照密钥字母顺序进行编号，按此顺序写出明文列，作为密文。

01248密码/云影密码

0表示间隔，其他数字相加表示在1-26中的字母下标。

键盘类

手机键盘

用手机键盘上的两位数字表示字母。
加密方式不可能以1开头，第二位数字不可能超过4。

电脑键盘坐标

三行字母，一个字母被加密成两个数字，即所在列和所在行。

电脑键盘QWE

即用字母序代替键盘序。

流密码

流密码一般逐字节或者逐比特处理信息。流加密目前来说都是对称加密。一般来说

流密码的密钥长度会与明文的长度相同。
流密码的密钥派生自一个较短的密钥，派生算法通常为一个伪随机数生成算法。

伪随机数生成器

伪随机数生成器（pseudorandom number generator，PRNG），又称为确定性随机位生成器（deterministic random bit generator，DRBG），是用来生成接近于绝对随机数序列的数字序列的算法。

定义 PRNG 的周期如下：对于一个 PRNG 的所有可能起始状态，不重复序列的最长长度。显然，对于一个 PRNG 来说，其周期不会大于其所有可能的状态。但是，需要注意的是，并不是当我们遇到重复的输出时，就可以认为是 PRNG 的周期，因为 PRNG 的状态一般都是大于输出的位数的。

线性同余生成器(LCG)

递归公式：
若，则周期
所以选取系数时应尽量使得a为模m的原根，以此尽量延长LCG的周期。

LCG

~~cao……突然发现就是当时moe密码的三个线性同余方程……离谱~~ dbtyyds!

基本上就是已知之后的随机数，求个初始值。
求出来a和b就可以……或者像dbt那道题根本不用求b……

或者考虑CTFwiki上的解法，根据模数和前两次随机数逆推出初始状态。
即依次从低比特位枚举到高比特位获取初始状态值，这个思路是基于以下观察：

a + b = c，c 的第 i 比特位的值只受 a 和 b 该比特位以及更低比特位的影响。因为第 i 比特位进行运算时，只有可能收到低比特位的进位数值。
a - b = c，c 的第 i 比特位的值只受 a 和 b 该比特位以及更低比特位的影响。因为第 i 比特位进行运算时，只有可能向低比特位的借位。
a * b = c，c 的第 i 比特位的值只受 a 和 b 该比特位以及更低比特位的影响。因为这可以视作多次加法。
a % b = c，c 的第 i 比特位的值只受 a 和 b 该比特位以及更低比特位的影响。因为这可视为多次进行减法。
a ^ b = c，c 的第 i 比特位的值只受 a 和 b 该比特位的影响。

思路如下：
1.依次从低比特位到高比特位依次枚举第一次迭代后的 x 的相应比特位。
2.根据自己枚举的值分别计算出第二次的值，只有当对应比特位正确，可以将其加入候选正确值。需要注意的是，这里由于取模，所以我们需要枚举到底减了多少次。
3.此外，在最终判断时，仍然需要确保对应的值满足一定要求，因为之前对减了多少次进行了枚举。

题目

线性反馈移位寄存器(LFSR)

这直接看wiki和track神的博客吧
~~一个一个抄公式太累了……~~

几点个人理解：
反馈函数：
其中，均在某个有限域中。
有限数域一般是，即只含有0, 1两个数。
实际代码实现中，用逐位异或可以代替加法和乘法，即取的逐比特异或。

实现代码
 题解

RC系列

RC2

参考资料

密钥扩展

字节密钥，置于数组中，使用一个固定的P盒。

for do
for do

最终有64字节密钥用于加密。

加解密

一次4字节加密，记为，分MIX和MASH两个过程。

MIX
定义
~
MIXING

RC4

RC4使用一个长度为256的s_box，一个长度任意的密钥（不大于256）。密钥的主要功能是将s_box搅乱，i保证s_box的每个元素都得到处理，j保证s_box的搅乱是随机的。将s_box与明文异或，得到密文。解密过程也完全相同。

RC4

RC5

密钥扩展

w - 一个字的长度（以bit为单位)，通常是16、32或64。加密以两个字为单位进行。
u＝w/8-一个字的长度，以字节为单位。
b-密钥的长度，字节为单位。
K[]-密钥，可以看作是一个由字节数据组成的数组(下标从0开始)。
c - 密钥的长度，以字为单位(如果b=0，取1).
L[] - 一个在密钥生成的临时数组，用来按字初始化密钥
r - 加密的轮数。
t=2(r+1) - 需要的轮加密的子密钥个数。
S[] - 伪随机S数组。

不同w对应不同的和。


16	0xB7E1	0x9E37
32	0xB7E15163	0x9E3779B9
64	0xB7E151628AED2A6B	0x9E3779B97F4A7C15

void RC5\_SETUP(unsigned char *K)
{
   // w = 32, r = 12, b = 16
   // c = max(1, ceil(8 * b/w))
   // t = 2 * (r+1)
   WORD i, j, k, u = w/8, A, B, L[c];
   
   for(i = b-1, L[c-1] = 0; i != -1; i--)
      L[i/u] = (L[i/u] << 8) + K[i];
   
   for(S[0] = P, i = 1; i < t; i++)
      S[i] = S[i-1] + Q;
   
   for(A = B = i = j = k = 0; k < 3 * t; k++, i = (i+1) % t, j = (j+1) % c)
   {
      A = S[i] = ROTL(S[i] + (A + B), 3);
      B = L[j] = ROTL(L[j] + (A + B), (A + B));
   }
}

加密

建议12或20轮。

#define ROTL(x,y) ((x<<(y&0x3f))|(x>>(64-y&0x3f)))
#define ROTR(x,y) ((x>>(y&0x3f))|(x<<(64-y&0x3f)))
//加密
void RC5\_ENCRYPT(WORD *pt, WORD *ct)
{
   WORD i, A = pt[0] + S[0], B = pt[1] + S[1];
   
   for(i = 1; i <= r; i++)
   {
      A = ROTL(A ^ B, B) + S[2*i];
      B = ROTL(B ^ A, A) + S[2*i + 1];
   }
   ct[0] = A; ct[1] = B;
}
//解密
void RC5\_DECRYPT(WORD *ct, WORD *pt)
{
   WORD i, B=ct[1], A=ct[0];
   
   for(i = r; i > 0; i--)
   {
      B = ROTR(B - S[2*i + 1], A) ^ A;
      A = ROTR(A - S[2*i], B) ^ B;
   }
   
   pt[1] = B - S[1]; pt[0] = A - S[0];
}

TEA系列

一种分组加密算法，此系列算法都使用了一个神秘常数作为倍数，程序中一般写作0x9E3779B9。但有时该常数会以减法的形式出现，即0x61C88647。
代码中均使用64bit(8byte)的明文作为加密数据，采用128bit(16byte)的值作为key，算法采用迭代的形式，推荐的迭代轮数是64轮，最少32轮，这里采用32轮。

TEA

XTEA

加密逻辑有所变化，对每轮加密的key的选择也有所变化。

XTEA

XXTEA

加密的明文数据可以不再是64bit（两个32位无符号整数），并且其加密轮数是由n即待加密数据个数决定的。由于n决定加密轮数，所以对于多组同时加密的数据不能分开解密，同时分开加密的数据也不能同时解密，要注意是一组数据是一起加密还是分开加密。

XXTEA

块加密

可以把块加密理解一种特殊的替代密码，但是其每次替代的是一大块。而正是由于一大块，明文空间巨大，而且对于不同的密钥，我们无法做一个表进行对应相应的密文，因此必须得有复杂的加解密算法来加解密明密文。

混淆，Confusion，将密文与密钥之间的统计关系变得尽可能复杂，使得攻击者即使获取了密文的一些统计特性，也无法推测密钥。
一般使用复杂的非线性变换可以得到很好的混淆效果，常见的方法：S盒、乘法

扩散，Diffusion，使得明文中的每一位影响密文中的许多位。
常见的方法有：线性变换、置换、移位，循环移位

ARX

ARX: Add-Rotate-Xor，即

Add 有限域上的模加
Rotate 循环移位
Xor 异或
执行时间为常数，可以避免基于时间的侧信道攻击，但是Rotate、Xor 对于单个 bit 来说均是完全线性的运算，可能会带来一定的脆弱性。Rotational cryptanalysis

DES

整体流程：
64bit划分为左右两部分L和R，R与key作为轮函数Feistel的参数，计算出结果与L异或，再交换左右两部分输出。此步骤进行16轮后，交换左右两部分，输出作为密文。

具体而言，在轮函数Feistel中，R要expand后与key异或，此后经过S盒混淆与P盒扩散，得到最终结果。

expand： 明文扩展，将32bit明文R扩展为48bit。具体而言，有一个置换表e，将明文中的32bit拆散后按此表的顺序拼接。由于是扩展到48bit，所以有的位会重复利用。
轮密钥加： 扩展后的明文R与key异或。
S盒混淆： 将48bit的字节流拆分为6bit一组，一共8组，在8个大小为64的S盒中查找相应的4bit字节拼接。此步骤将48bit的字节重新还原为32bit。
P盒扩散： 同样是查表替换，按序拼接。
密钥扩展： 使用64bit的key中的56bit，后8位要么丢弃，要么作为校验位。对这64bit密钥查表置换为56bit，然后拆分为左右两部分l和r。
循环左移1或2位（根据offset表决定），查表得到48bit的密钥。此步骤重复16轮，得到16轮加密的子密钥。

DES

IDEA

加密64bit数据块，使用128bit长度的密钥，对输入的数据块进行9轮变换。每轮使用6个16bit密钥，最后一轮使用4个。
前8个密钥来自初始密钥，从到依次从高到低取16bit。密钥循环左移25位获取下一轮密钥，然后再次分为8组

1.对块与密钥模乘得到，块与密钥模加得到，两者异或得到。
2.对块与密钥模加得到，块与密钥模乘得到，两者异或得到。
3.与密钥模乘得到，与模加再与模乘得到，与模加得到。
4.与异或得到，与异或得到，与异或得到，与异或得到。
5.重复7轮上述操作。
~~捋一遍真的累死~~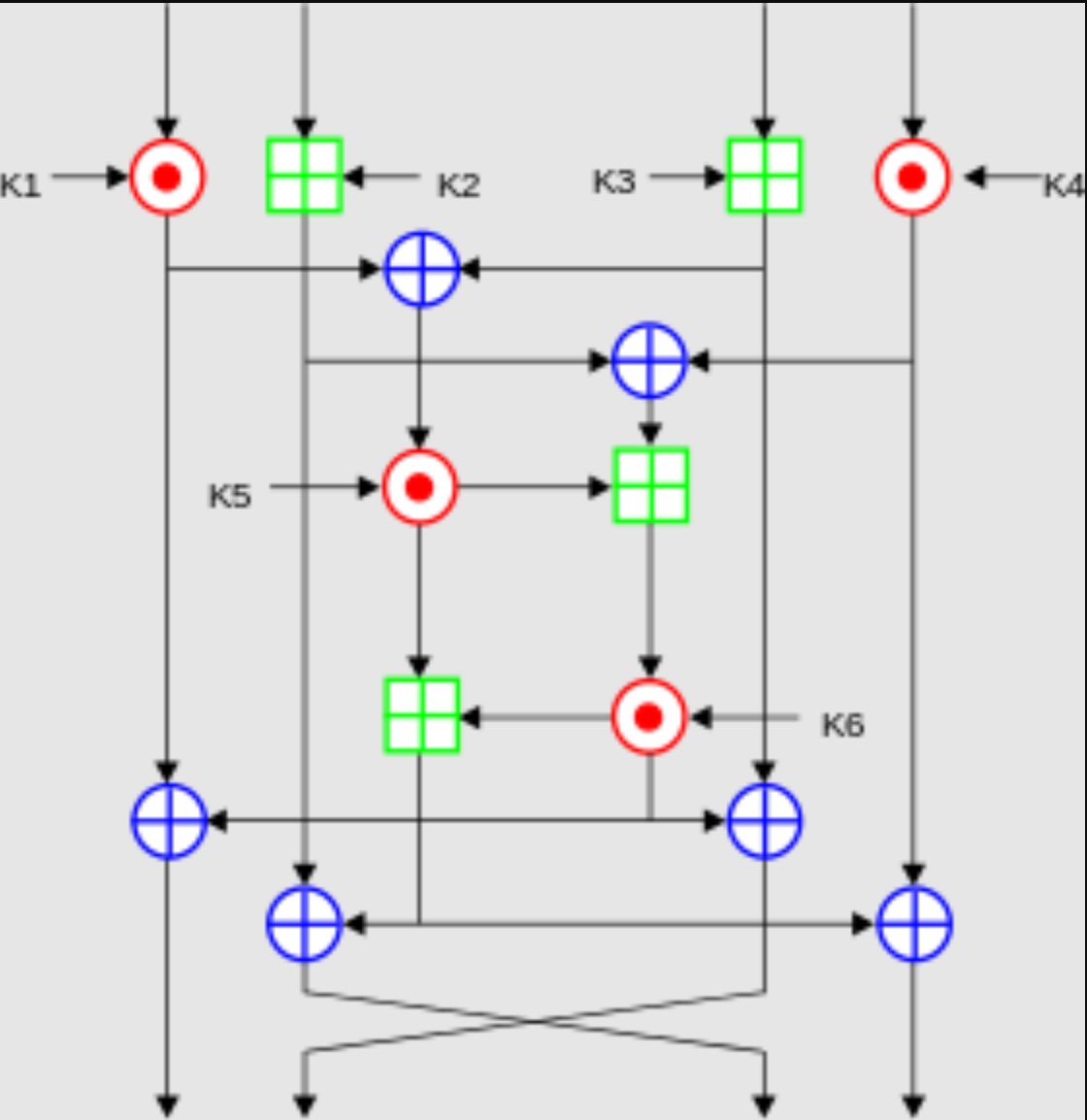

6.最后一轮中，块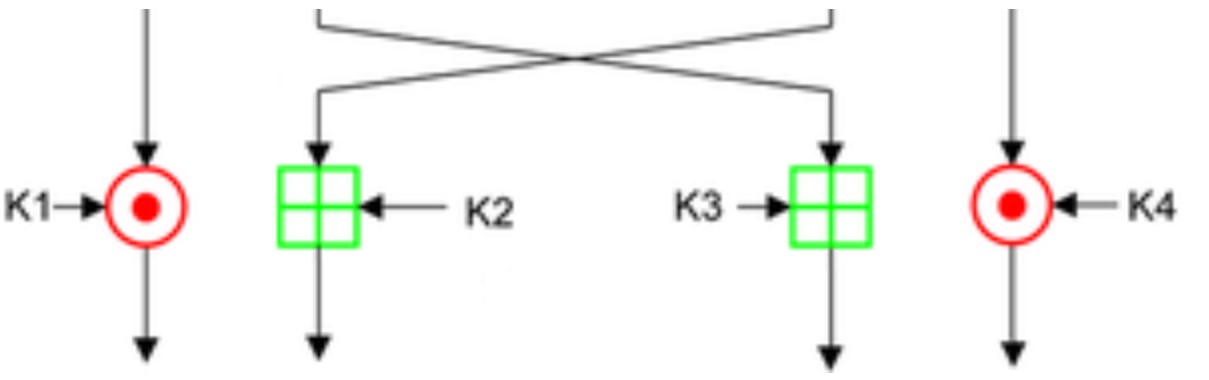与密钥模乘得到，块与密钥模加得到，块与密钥模乘得到，块与密钥模乘得到，

其中模加的模数为，模乘的模数为。注意0x00的输入会被修改为，的输出结果会被修改为0x00。

解密流程的逆元选取：
1~9轮的解密密钥的前4个子密钥由加密过程中第轮的前4个子密钥得出
其中第1个和第4个解密子密钥为相应的子密钥关于的乘法逆元。
第2个和第3个子密钥的取法：
当轮数为2~8时，取相应的第3个和第2个的子密钥的的加密逆元。
当轮数为1或9时，取相应的第2个和第3个子密钥对应的的加密逆元。
第5和第6个密钥不变。

AES

明文分块后转为4*4矩阵，一块是128bit，一个元素一字节。其排列顺序顺序为从上到下，从左到右。

1.轮密钥加

2.1.字节替换
将矩阵中每个字符在S盒中的映射进行替换
2.2.行移位
第i行循环左移i位
2.3.列混合
每一列乘以一个矩阵，得到新的一列密文
2.4.轮密钥加
与轮密钥异或

3.重复2若干轮（10，12，14）

4.1.字节替换
4.2.行移位
4.3.轮密钥加

AES

SM4

输入4*4字节明文，32轮迭代后输出反序作为密文。
每一轮迭代需要4字节轮密钥，迭代过程即是不断使用轮函数F，往后计算下一个字。

例如4字明文，一轮迭代后得到
二轮迭代即是
以此类推，得到，输出作为密文

轮函数执行的运算为：

合成置换T：
一字输入A，一字输出C，包含非线性变换和线性变换，即

非线性变换:
对输入的4字节每个字节进行S盒替换

线性变换：

密钥扩展：
1.异或
每个字与系统参数异或得到
系统参数：
2.轮迭代

以此类推计算32此轮密钥，其中类似于T，只是线性变换有所变化：

3.计算
长4字节，表示为
为第个的第个字节，其构造方法为
即实际为一组已知的常量。

Simon and Speck

Block size(bits)	Key size(bits)	Rounds
32	64	32
48	72	36
	96	36
64	96	42
	128	44
96	96	52
	144	54
128	128	68
	192	69
	256	72

每轮加密算法一样，如下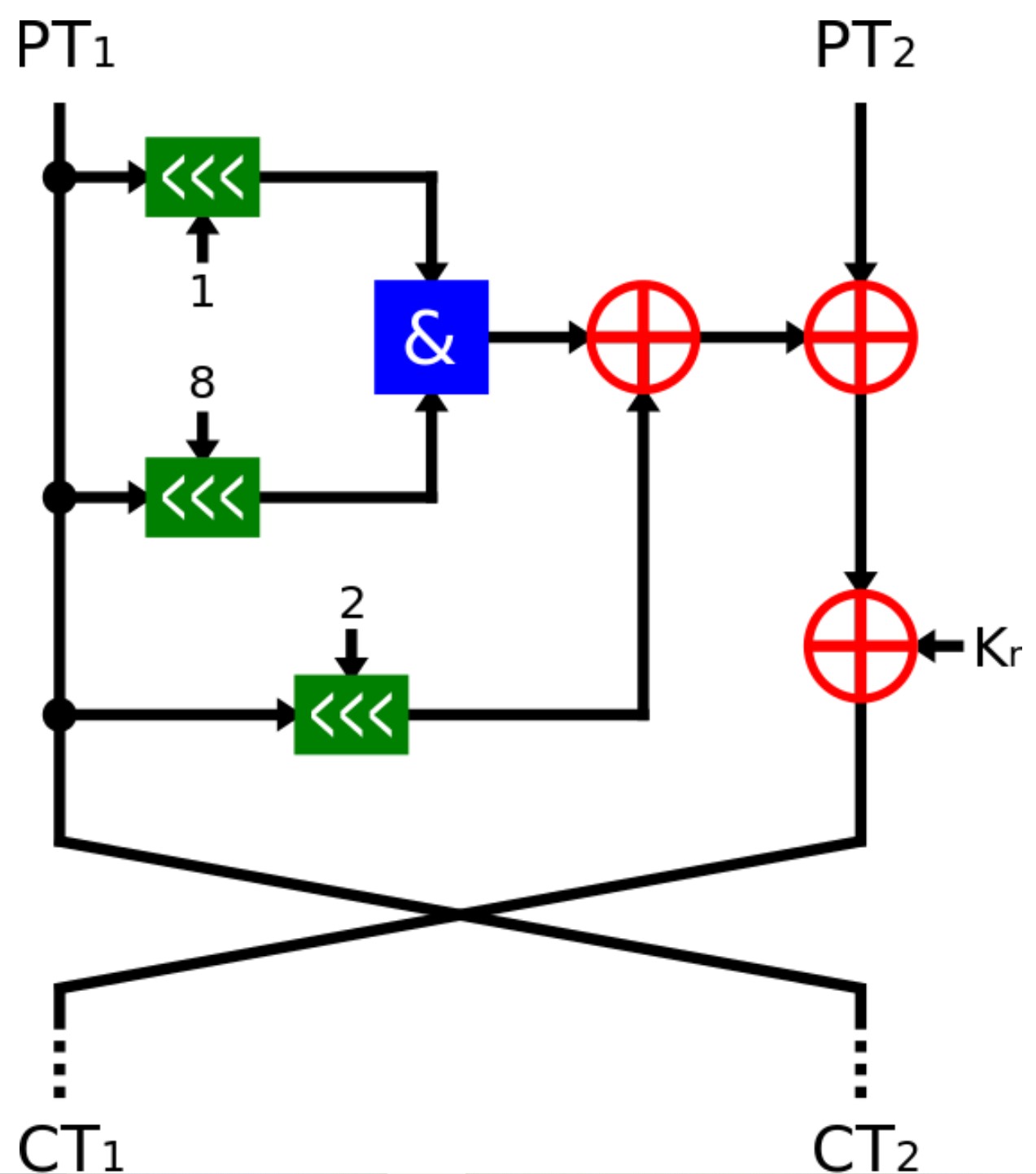

当然，对于每一轮以及不同的 m 来说，密钥也会有所不同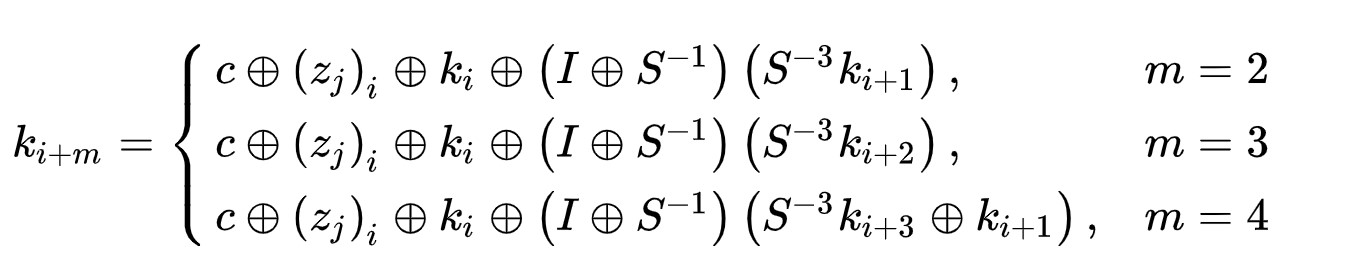

其中，是由LFSR生成的，虽然对于不同的的逻辑不同，但是初始向量是固定的。

Constant

Simon

blowfish

分组模式

padding

即使消息的长度是块大小的整数倍，仍然需要填充。
一般来说，如果在解密之后发现 Padding 不正确，则往往会抛出异常。我们也因此可以知道 Padding 是否正确。

1.用缺少的字节数的十六进制填充
2.下一个填0x80，往后填0
3.填0，最后一个字节填缺少的字节数的十六进制
4.全部填0
5.空白(0x20)填充

ECB

电子密码本模式(Electronic codebook)，直接划分明文块加密。

CBC

密码分组链接（Cipher-block chaining）

IV 不要求保密
IV 必须是不可预测的，而且要保证完整性。

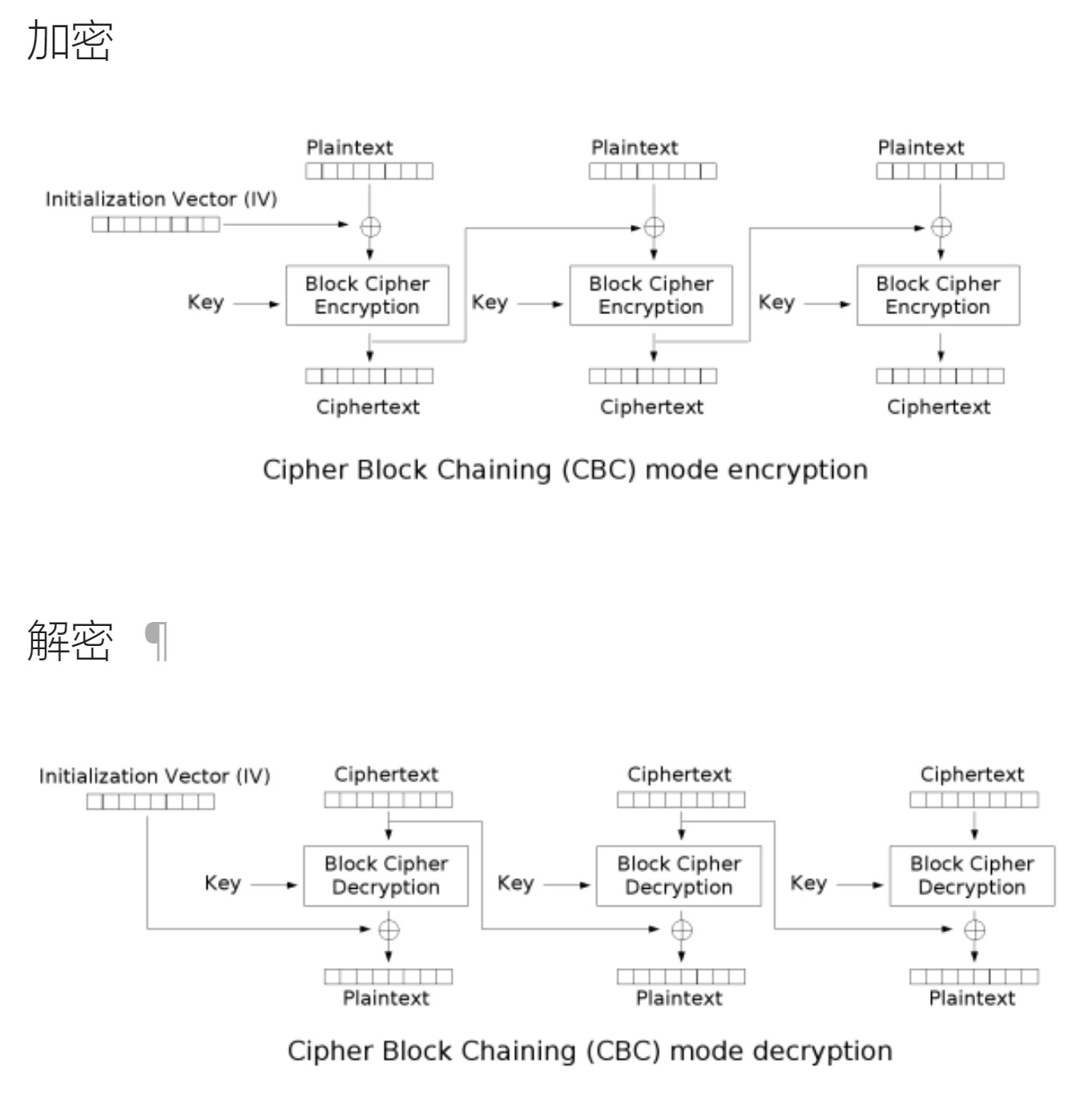
字节反转攻击：
对某个信息已知的原文和密文，修改第个密文块为，然后解密，那么第个明文块将变成A。

PCBC

明文密码块链接（Plaintext cipher-block chaining），也称为填充密码块链接（Propagating cipher-block chaining）。

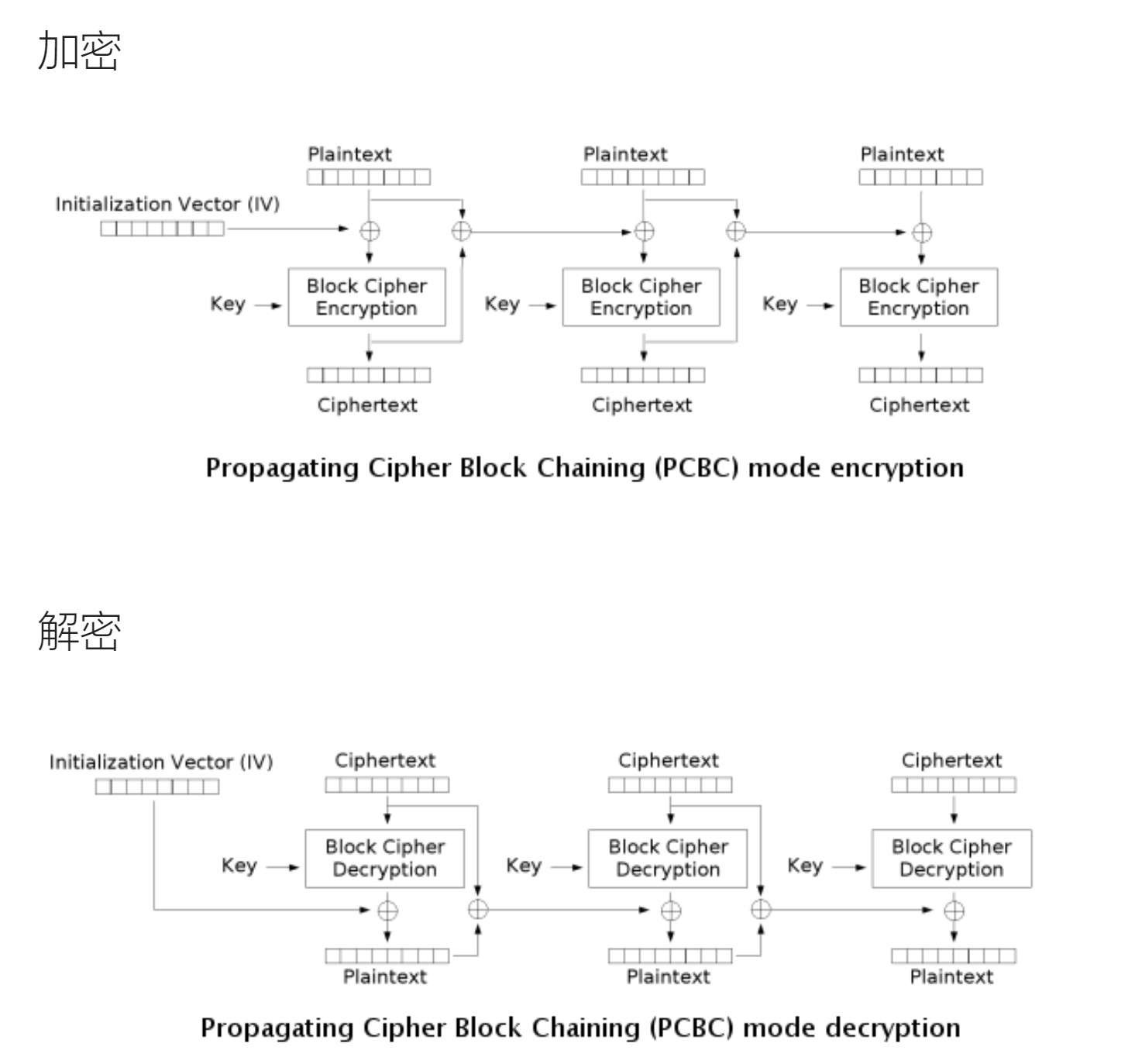
互换邻接的密文块不会对后面的密文块造成影响

CFB

密文反馈模式（Cipher feedback）。

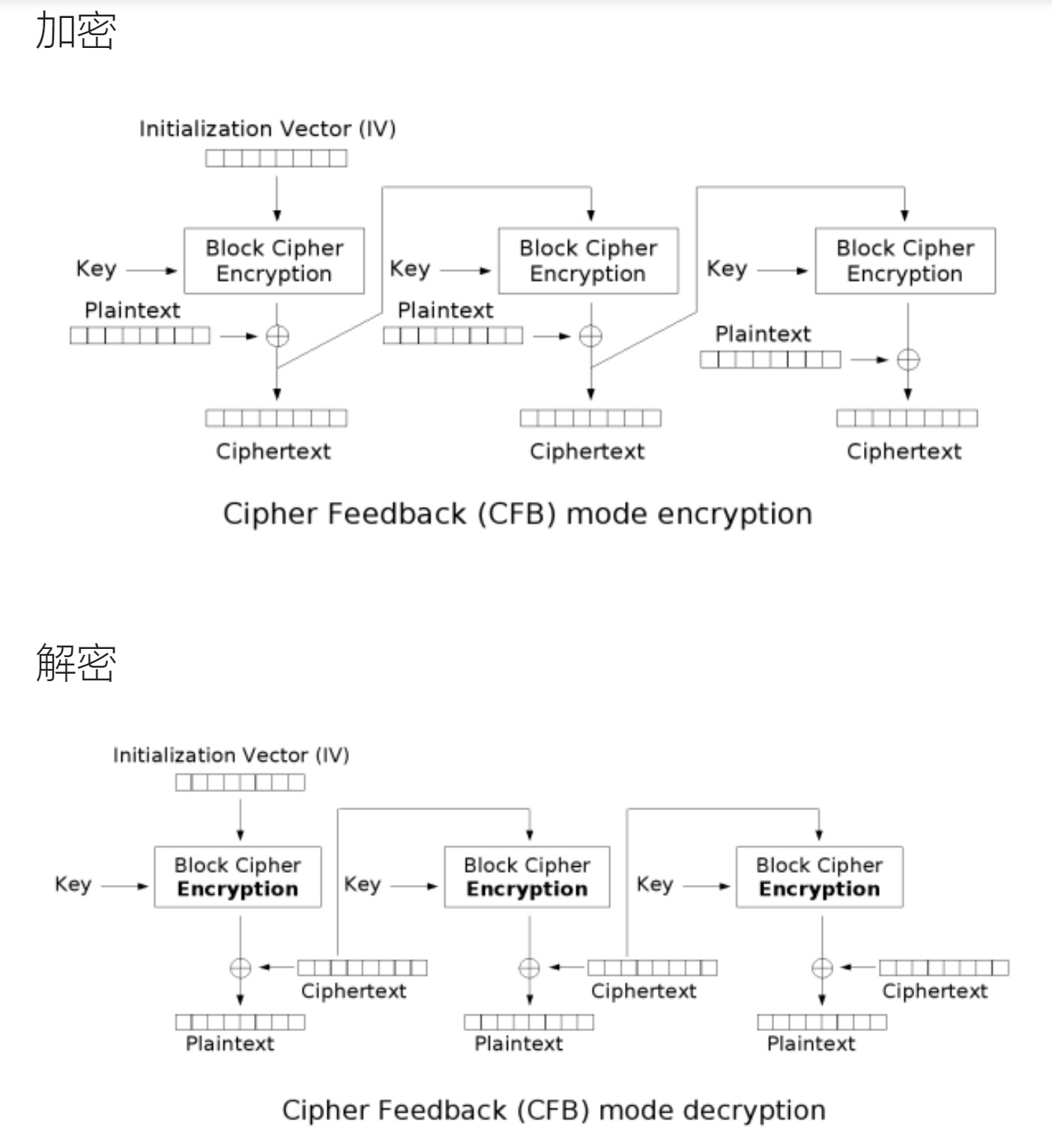
OFB

输出反馈模式（Output feedback），其反馈内容是分组加密后的内容而不是密文。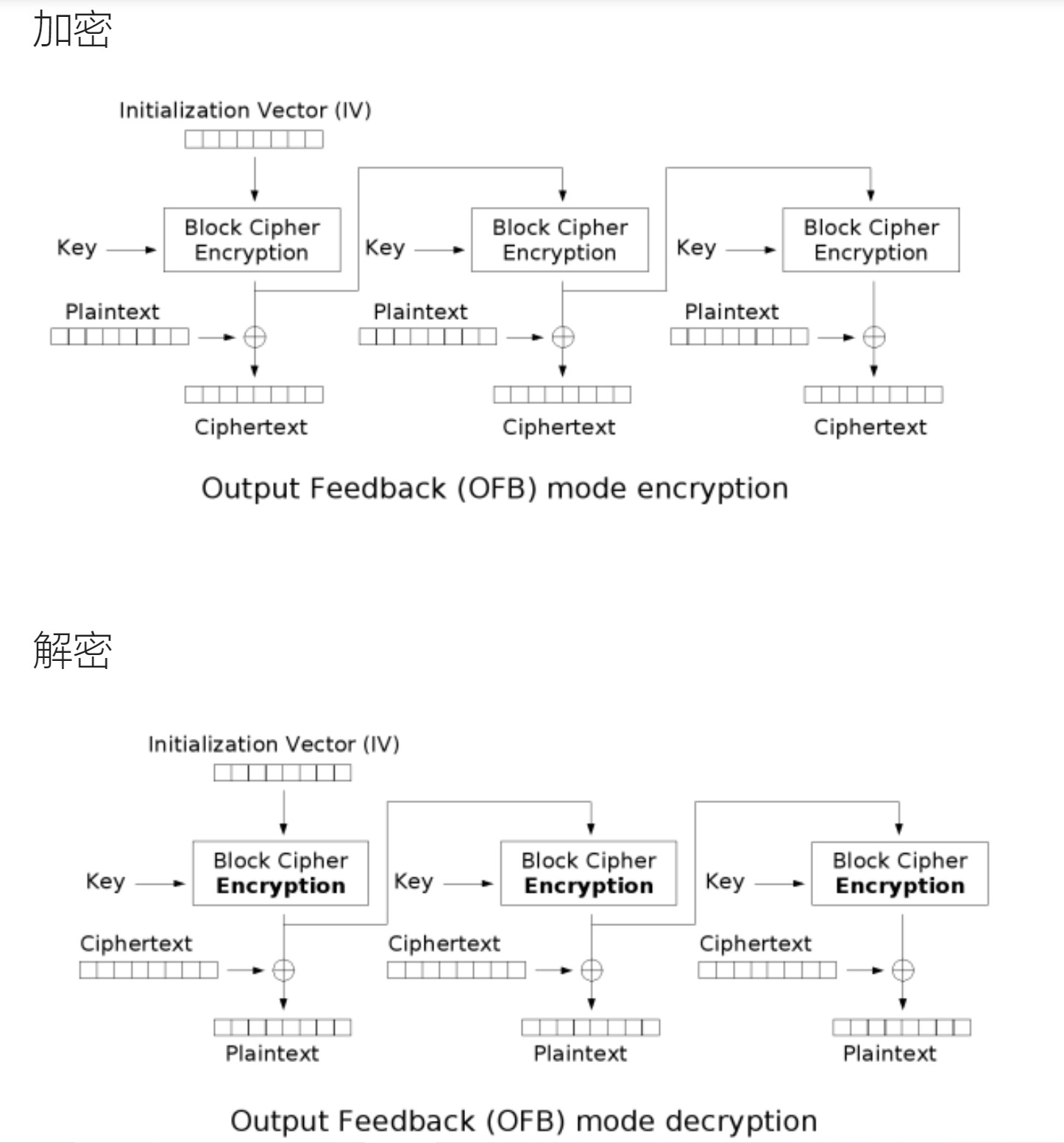

CRT

计数器模式（Counter mode）。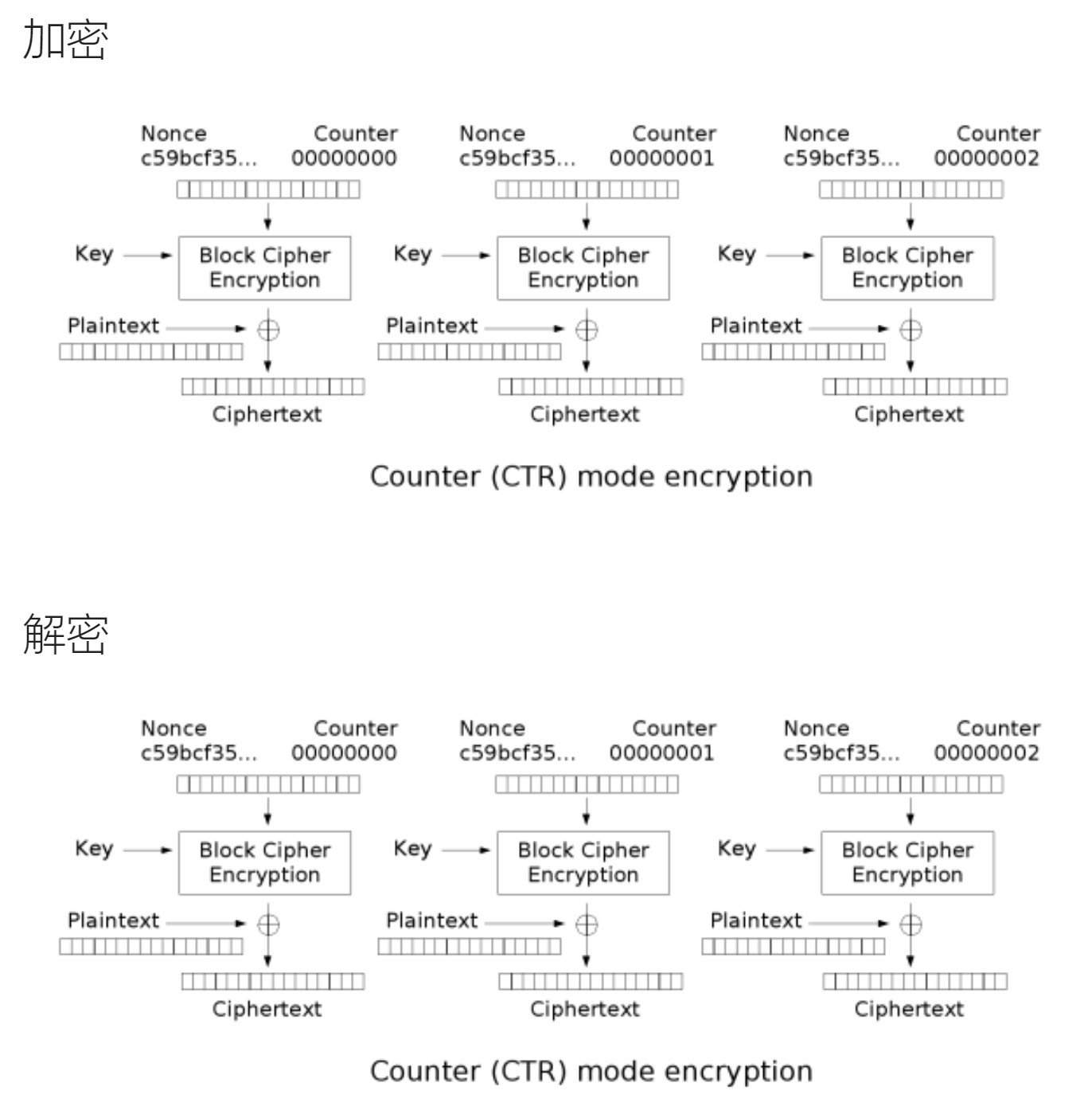

非对称加密

咕

哈希函数

MD2

MD5

SHA1

SHA256

校验

CRC

CRC.py

常用的CRC码生成多项式：

每一个生成多项式都可以与一个代码相对应，如CRC8对应代码：100110001
从低位到高位是从0到x(假设是CRCx)

设原始数据为
1.找到CRC的对应二进制串crc
2.左移位得到，求对crc的模2除法的余数（或依次按位异或）得到余数
3.发送，即串追加串的结果。
4.接收端对此串除以crc，余数为0则无差错。

关于本文

本文作者云之君, 许可由 CC BY-NC 4.0.